3DISO: Adapting Isometric Scrolling Theory to 3D Worldspace, Part 3

February 18, 2002
by Andrew M. Phelps

Part 1 of this article discussed some of the impetus behind moving our existing isometric engine over to Shockwave 3D, and the basic theory behind scrolling games.

In Part 2 we went into the math behind scrolling, and introduced the concept of isometric landscapes.

Sample Director 8.5 movie source is available for download in ZIP or SIT archive format (both files are approximately 1.2MB). If you have Shockwave 8.5, you can view the 3DISO engine (~185K).

3 Isometric Landscapes (continued)

3.2 Implementation of the Isometric View

Given that an Isometric environment requires the entire screen space to be filled with tiles, lining them up in a scheme designed to cover the entire area is critical. There are 3 major schemes for accomplishing this task, each with advantages and disadvantages. The first of these schemes involves using the tiles to create essentially one large tile (see figure 12), which has the advantage of the easiest numbering system with regard to the tile space, but tends to waste a large number of tiles relative to the viewable area (if all are drawn). This is commonly referred to as the diamond map, and is used in smaller Web-based sims. It can suffer from performance drawbacks without a well-optimized clipping algorithm, as many tiles fall outside the viewable area

The second scheme, the column map, involves numbering the tiles in a zig-zag pattern (see figure 12). This covers the screen with the smallest number of tiles, and thus would theoretically operate the fastest, but the movement of the charac-ter is more difficult to calculate. Essentially, a character will move 2 units on the cardinal directions (up, down, left, right) and 1 unit on the diagonal. To further compound the issue, lateral movement doesn't necessarily change the first coordinate value. An algorithm to accomplish such a movement will likely examine the current position of the character, determine if the character is currently on an odd or an even row, and then adjust the CurrentPosX and CurrentPosY variables accordingly.

The final solution, the slide map, is possibly the easiest to navigate and render, but is of limited utility due primarily in the difficulty in creating meaningful level creation tools. In a slide map, x increases to the east, and y to the southeast, so programmers generally regard the movement algorithms as cumbersome the first time through. To move south, for example, involves a tile plot one tile west and 2 tiles south-east. Implementing collision detection and path plotting on top of a system like this is cumbersome, and so slide maps are generally reserved for quick scrolling action games that choose speed over accuracy (as opposed to, say, strategy sims).

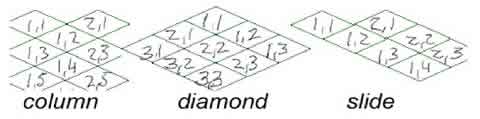
Figure 13: Tiling schemes for isometric engines

Andrew (Andy!) is a professor at the Rochester Institute of Technology (RIT) serving in the Dept. of Information Technology, specializing in Multimedia and Web Programming. While completing his MS in Information Technology, he became increasingly interested in multi-user virtual spaces. He is also developing a game programming curriculum, with an emphasis on Lingo based solutions as well as more traditional approaches. Visit his home at andysgi.rit.edu.