Checking for the Mouse inside a Triangle

June 14, 2002
by Will Turnage

Dear Multimedia Handyman,

I'm making a game where the tiles are triangular. They stand close to each other, which means that the coordinates (rect) intersect. I need to be able to click on each of these sprites independently. I'm also using imaging Lingo, so I can't check the rollover for different sprites. How can I determine which tile the cursor is over?

Best Regards,
Torstein Soerlid

Dear Torstein,

This one's a little tough to figure out. Luckily, I did some searching around the web and some college math departments were able to help me out. The first step is that you need a way to mathematically calculate the area of any triangle. The following handler allows you to pass three separate points, and it will calculate the area encompassing all three points:

on returnTriangleArea pointOne, pointTwo, pointThree

  a = (pointOne.locH - pointThree.locH)
  b = (pointOne.locV - pointThree.locV)
  c = (pointTwo.locH- pointThree.locH)
  d = (pointTwo.locV - pointThree.locV)
  return (0.5 * abs ((a*d) - (b*c)))

end

For this handler, all you have to do is pass it three separate points. The handler then calculates the difference in locH and locV of the different points of the triangle and returns the final area to your original function. For instance,

put returnTriangleArea (point (191, 5), point (133, 107), point (252, 107))
-- 6069.0000

So if you want to check if a point is inside a triangle, then here's how you do it. First you take the point that you are checking, and using that point you divide the original triangle into three separate triangles. Next you calculate the areas of each of these three smaller triangles. If the sum of the areas of these three smaller triangles is equal to the area of the original triangle, then the point is inside the triangle. If the sum of the areas of the three smaller triangles is greater than the area of the original triangle, then that means the point is outside the triangle. Confused yet? Look at this picture:

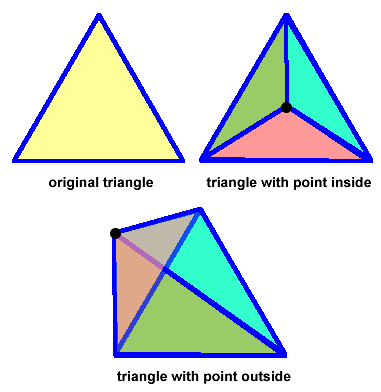
The triangle on the left is the original triangle. If a point is inside the triangle, then the sum of the three smaller triangles formed by this point is equal to the area of the original triangle. However, if a point is outside the triangle, then the sum of the areas of the three smaller triangles is greater than the area of the original triangle.

Now, let's convert all of this talk into Lingo.

on insideTriangle checkPoint, trianglePointOne, trianglePointTwo, trianglePointThree

  areaOne = returnTriangleArea (checkPoint, trianglePointTwo, trianglePointThree)
  areaTwo = returnTriangleArea (checkPoint, trianglePointOne, trianglePointThree)
  areaThree = returnTriangleArea (checkPoint, trianglePointOne, trianglePointTwo)
  triangleArea = returnTriangleArea (trianglePointOne, trianglePointTwo, trianglePointThree)
  if ((areaOne + areaTwo + areaThree) > triangleArea) then
    return false
  else
    return true
  end if

end

This handler is passed four points. The first point is the point that you are checking, and the next three points are the three points of the main triangle. Next you calculate the areas for the four possible triangles. Finally, you check to see if the sum of the three smaller triangles is greater than the sum of the original triangle. If it is, then you return false, meaning that the point is not inside the triangle. Otherwise, you return true.

When you put it all together, you can get a movie that works like this.

A sample Director 8.5 movie is available for download in ZIP or SIT archive format.

All colorized Lingo code samples have been processed by Dave Mennenoh's brilliant HTMLingo Xtra, available from his site at http://www.crackconspiracy.com/~davem/

Will Turnage is a multimedia programmer based in New York City. In addition to his weekly role as Director Online's Multimedia Handyman, he is also the Technology Director for Sony Music's Client Side Technologies Group. You can read more about his work at http://will.turnage.com/.