The physics of an elastic collision: Part I

November 22, 1999
by Raman Pfaff

In my last article we learned how to deal with a gravitation force in Lingo so that we could simulate a football getting tossed around, a feather dropping from the sky, or a hammer dropping on your foot. That may seem interesting to some, but after a brew or two, an evening involving billiards might seem more interesting. Pool is a game of collisions (visiting the local pool hall while teaching a physics course is always worthwhile). When I first started creating simulations with Director I realized I really need to understand the physics underlying each particular experiment. Since the goal of this two part article is to write a basic simulation of pool, we'd better try to learn a bit about the physics of a collision!

Pop Quiz

Let's think about a few basic collisions involving an elephant and myself. (When teaching I would break you all into small groups and let you discuss these questions amongst yourselves.)

Suppose I am standing on the side of the road (velocity = 0) and an elephant runs directly into me. What will happen to me (in particular my velocity)? What will happen to the elephant and its velocity? If I run directly into a stationary elephant what will happen to my velocity? What will happen to the velocity of the elephant? An elephant and I run straight at one another. What happens to our velocities?

Momentum

We'll get to the answers for the pop quiz, but first let me introduce the term momentum, which is a rather valued commodity in the world of physics. Momentum (generally abbreviated as P) is defined to be the mass of an object multiplied by the velocity of the object. This can be written as

Momentum can be large or small, as well as positive or negative. This is known as a vector - it has a magnitude (size), and a direction. Velocity is also a vector (i.e. I'm driving North at 55 miles per hour). In Equation 1 the vector is indicated by the small line above the P and the v. Mass is not a vector (it only has a magnitude, not a direction).

In my last lecture (a.k.a. my previous article) we discussed the fact that you can have a velocity to the right (a positive Vx), a velocity down (negative Vy), etc. Momentum "moves" in the same direction as the velocity. By now I'm sure you are saying "Why are telling me all this stuff?" Here is the reason: In a collision, the momentum of a system is conserved (i.e. the total momentum of the system is the same after the collision as it was before the collision - or as I like to say, what goes in must come out). A "system" consists of the two particles that are colliding. We can write this as

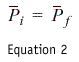
where the i and the f indicate initial and final (recall that P is momentum).

Here are several examples of momentum.

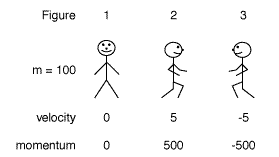
In Figure 1 I am standing on the road. My velocity is zero. My mass is 100 kg. I then find that P = 0*100 = 0 (although I would punish my student for doing this, I am going to skip the 'units' associated with momentum). I have no momentum. In Figure 2 I am running to the right at 10 m/s. My mass is still 100 kg. I then find that P = 1000. I am running to the left at 5 m/s in Figure 3 and my mass (despite all this running) is still 100 kg. My momentum is now P = (-5)*(100) = -500, since I have defined the positive direction to be motion to the right, and negative is to the left.

Back to the quiz

For question 1, I think that if an elephant ran directly in to me I would go flying backwards, and the elephant wouldn't really notice the collision. My students enjoy this question when I do a "stunt" fall over a table as the virtual elephant runs me down. O.K., lets now think about me and the elephant in terms of momentum. There are two things in our "system," me and the elephant. I am not moving, so my momentum is zero. The elephant is running at me. Let's say the elephant is moving at 5 m/s, and has a mass of 1000 kg. The initial momentum of the system = Pme + Pelephant = 0 + 5000 = 5000 (the total momentum before the collision).

After the collision the total momentum must be equal to 5000 due to the Law of Momentum Conservation. Since I think I will be moving with a high velocity to the right I can say that I have some positive momentum which is greater than my initial momentum of zero. Thus, the elephant must now have less momentum (it got slowed down a bit when it collided with me). How much did it slow down? To answer this question we need to introduce one more physics term (I promise it is the last new term for the day).

Energy

The term energy is used in many ways ranging from people showing up for work on Monday morning saying "I have no energy," to chemists discussing the energy levels of a newly discovered element. For introductory physics (and this article) we only need to know about kinetic energy (KE), which is often referred to as the energy of motion. If something is moving, it has kinetic energy, and if it not moving it has no kinetic energy. It is defined as

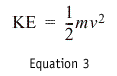
where m is the mass of the particle, and v is the velocity of the particle. Kinetic energy is not a vector (it can be large or small, but does not have a direction associated with it). In an elastic collision the kinetic energy is conserved: the initial kinetic energy of the system is equal to the final kinetic energy. We now have two conservation equations that will let us determine the final velocities of two colliding particles if we know their initial velocities and masses.

I know nothing...

As a graduate student I hated doing homework, so I would often use a line such as "using Gauss-Jordan elimination, I find that..." which really meant I had found the answer somewhere else and didn't want to go through thirty pages of derivation, so in that vain we will jump to the summary of this momentum and energy conservation dance that occurs during a collision. The derivation starts with the momentum and energy conservation statements.

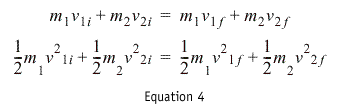
where the i's indicate initial values, the f's indicate final values, and the v's are the velocities. I then proceed to do a bit of algebra, and find that the final velocities of the particles can be given by

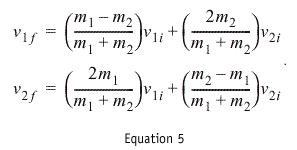
As I said before, I now know exactly how quickly the particles are moving after they collide if I know the initial velocities and masses.

Lingo, me, and an elephant

It is apparent that mass is involved in all these equations, so I begin editing the code from my previous article and add a property to deal with the mass.

property myMass

That seemed easy enough. I also added a statement to the property description so that the user can set the mass when slapping the behavior on me and the elephant.

addprop des,#myMass,[#default:1.0,#format:#float,¬
  #comment:"Mass?"]

The other term I've used throughout this article is "collision." We will have to detect the collision (the time when particles touch for the first time), and we will have to tell the particles what their new velocities should be after the collision. In order to deal with the latter I add a new handler to the Gravitational Force behavior:

on changeMyVelocity me,newVx,newVy
  set vx = newVx
  set vy = newVy
end

Once I have detected a collision between two particles (sprites) I can use Equation 5 to solve for the new velocities, but to use the equation I will need to know the mass of each particle, and the velocity of each particle, so I add a second handler to the behavior which will return a list with the mass, x velocity, and y velocity of the particle.

on reportMyInformation me
  set tempList = []
  add tempList, myMass
  add tempList, vx
  add tempList, vy
  
  return tempList
  
end

The behavior is now complete. To detect the collision I will check the location of my two particles in a frame script. If the particle are within a "striking" distance I will implement Equation 5, find the new velocities, and tell the two particles to change their velocities. In this article the collision detection will just see if the particles (sprites) overlap by using the intersect lingo function (in Part 2 of this article we will change this functionality). I place my two moving particles in channel 7 and 8, so my frame script is written as

on exitFrame
  -- I place this frame script in a frame labelled 
  -- "before collision"
  if intersect(the rect of sprite 7, the rect of ¬
    sprite 8) = rect(0, 0, 0, 0) then
    nothing
  else
    dealWithCollision(7,8)
  end if
  
  go to the frame
  
end

The final piece to this puzzle involves the dealWithCollision movie script that I have called in the exitFrame when the two objects collide. This is where I must make use of Equation 5 where if you look a bit more closely at it (here comes the tough part) you'll notice there are no x's or y's associated with the velocity terms, but we know that velocity is a vector and has a direction associated with it. In Equation 5 I only showed two equations but to deal with the 2-dimensional world we have to use two equations for the x-direction, and two equations for the y-direction. As was mentioned in the previous article, the x- and y-motion are independent of each other (they each "do" their own thing). The movie script works as follows:

  -- you request the mass and current velocity 
  -- from the two sprites involved in the collision
  
  set infoList1 = sendSprite(sprite1,#reportMyInformation)
  set infoList2 = sendSprite(sprite2,#reportMyInformation)
  
  -- you then extract the information from the lists 
  -- that were returned
  set m1 = getat(infoList1,1)
  set m2 = getat(infoList2,1)
  
  -- the v stands for velocity, the i stands for intial, 
  -- the f stands for final, and x and y are the 
  -- two directions
  
  set v1ix = getat(infoList1,2)
  set v2ix = getat(infoList2,2)
  set v1iy = getat(infoList1,3)
  set v2iy = getat(infoList2,3)
  set massTot = m1+m2
  
  -- the next four equations represent Equation 5 from 
  -- the text the first two deal with the x-direction, 
  -- the second two deal with the y-direction
  
  set v1fx = ((m1-m2)*v1ix + 2*m2*v2ix)/massTot
  set v2fx = (2*m1*v1ix + (m2-m1)*v2ix)/massTot
  set v1fy = ((m1-m2)*v1iy + 2*m2*v2iy)/massTot 
  set v2fy = (2*m1*v1iy + (m2-m1)*v2iy)/massTot
  
  -- I now tell the two sprites to change their velocities
  sendSprite(sprite1,#changeMyVelocity,v1fx,v1fy)
  sendSprite(sprite2,#changeMyVelocity,v2fx,v2fy)

Have you made it this far? I'm not even sure if I have. We now have enough tools to do a full collision, but here are a few more details important to all of this. In this first article the equations are becoming rather ominous, but things are still not quite set for 2-dimensional collisions, so we will stick to 1-D collisions today (such as an air track experiment, or an elephant running in to me). When an apple sits on my desk, or an elephant stands on the ground, its acceleration is equal to zero (I promised not to introduce more physics terms, so I won't mention Normal Forces), and in the behavior I will be sure that I choose that value.

Also, after the collision occurs (I make the call to the dealWithCollision handler), I am going to jump to a different frame where I will wait until the particles have "separated," since we never want a collision to occur and have the dealWithCollision handler called while the two particle still overlap (this could lead to the particles getting "stuck" bouncing back and forth within each other). To do this I add a line after the dealWithCollision line which says

go to "after collision"

and in frame named "after collision" I add a frame script which will wait for the particles to separate (by waiting until the intersect function returns an empty rectangle), and then go back to the frame labelled "before collision" where the whole process will begin once again.

Pop Quiz Answers

Let's now look at the answers to the pop quiz using the code that we have now written. Click Start to see the answer to the three questions in a visuale mode. Do the results agree with your initial answers to the questions?

1-D is done...2-D is next

We've now gone through the code required for a 1-dimensional elastic collision. In the second part of this article we will migrate upward to a full 2-D elastic collision in an effort to create a game of pool which will require a more sophisticated method of collision detection, some added code to determine the angle of the collision, and a frame script that won't have to jump to another frame after a collision has occurred.

Sample movies are available for download in a Mac or PC format.

Copyright 1997-2024, Director Online. Article content copyright by respective authors.