Steering with Momentum

February 6, 2000
by Pat McClellan

I'm doing a driving game based on last week's Handyman article. I have the car driving round the track ok, except that it's not realistic - there's no inertia to give an acceleration effect, and no momentum, so it just stops dead when I take my finger off the accelarate key. Have you any tips?

Andrew

Dear Andrew,

I'm happy to help with the momentum, acceleration, drag (coasting) and braking. I'm going to leave it to you to figure out how to constrain the car to the track (assuming that's what you want to do.) I leave it to you because, frankly, I'm not sure how I'd do it. While the constraint of sprite property could keep the car over the rect of the track sprite, that doesn't keep it on the track itself. So, I think I'd try to do it mathmatically and use that instead of the constraining rect of last week's Steering behavior. For those of you who didn't read that article, I'd strongly suggest you do so now because I'll be using that behavior as a starting point for this article.

A sample movie is available for download in Mac or PC format. This is a D7 movie.

In last week's article, I spent a lot of time on the rotation angle of the moving sprite (the car). Rather than having to calculate the angle and X,Y change for each frame, I chose to create a lookup table. This take a little more time at the beginning, but can potentially speed up the frame to frame performance. In the beginSprite handler, we called the handler makeTrigList which built a list of X,Y values which are added or subtracted from the sprite's loc. In that behavior, we had a constant speed, so I just multiplied the speed as I was generating that list. However, if the speed is going to be variable (accelerating upwards and coasting or braking downward) then we'll want to leave speed out of the makeTrigList handler. I've indicated where I omitted it with a comment below.


on makeTrigList me
  pTrigList = []
  increment = (pi * 2)/pAngleSegments
  f = 0.0
  angle = 0
  repeat while f < (pi * 2)
    hFactor = sin(f) 
    vFactor = cos(f) * - 1
    
    -- speed was omitted from the next line
    hvList = [hFactor,vFactor]
    add pTrigList, hvList
    f = f + increment
  end repeat
  
end makeTrigList

To simulate momentum, we'll need to include acceleration, drag, and braking. We should also have a speed limit. All of these will be new properties in our new Steering w/ Momentum Behavior.

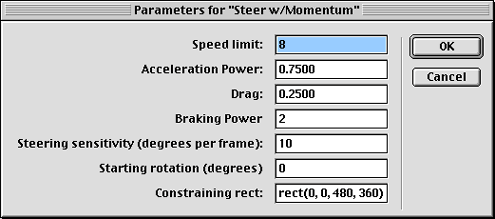
We'll need some new keyboard controls. J and L are still fine for the rotation. (I don't use arrow keys in Shockwave movies because some browsers reserve those keys for their own functionality -- like scrolling.) The I key will still work for applying forward thrust. But now, we need the K key for the brake. In order to thrust backwards -- which will either slow your forward motion or cause backward motion -- we'll use a keyboard combination, Control + I. All of these controls go into the exitFrame handler:


on exitFrame me
  -- rotation controls
  if keyPressed(37) then 
    rotate me, #clockwise
  else if keyPressed(38) then 
    rotate me, #counterclockwise
  end if
  
  -- thrust, brake, coast, thrustBack controls
  if keyPressed(34) then 
  
    if the controlDown then 
      moveSprite me, #thrustBack
    else 
      moveSprite me, #thrust
    end if   
    
  else 
  
    if keyPressed(40) then 
      moveSprite me, #brake
    else 
      moveSprite me, #coast
    end if
    
  end if
  
end exitFrame

Note that all of the if-then-else statements are carefully constructed to allow for rotation and motion at the same time, but not for rotation or motion in more than one direction at a time. This exitFrame handler doesn't actually rotate or move the sprite, but rather calls on other handlers in the behavior to do so. Again, the rotate handler wasn't altered at all from last week's article, so we'll just focus on the moveSprite handler next.

First we retrieve our XY vectors from the lookup table, pTrigList. We'll be multiplying these values by our pSpeed, but first we'll need to determine what that speed is going to be (based on whether it is thrusting forward, thrusting backward, coasting, or braking). To thrust forward (accelerate) then we simply add the pThrust value to the current pSpeed. This will cause it to cumulatively raise on each subsequent frame. The min() function just makes sure that pSpeed doesn't exceed our pTopSpeed (speed limit).

ThrustBack does just the opposite, although I've limited the backward speed to half of our forward speed limit -- just because it's more dangerous to drive backward. Brake subtracts the pBrakePower value from the pSpeed (or adds it if the car is moving backwards), and coast does the same, but with the much lower power of the pDrag value. After pSpeed is set, the move is calculated, the newLoc is checked against the bounding rect, and the sprite moves.


on moveSprite me, whichCommand
  -- convert angle to list index
  whichIndex = (pRotation/pAngle) + 1
  thisMoveXY = pTrigList[whichIndex]
  
  -- adjust speed
  case whichCommand of
    #thrust: pSpeed = min(pSpeed + pThrust, pTopSpeed)
    #thrustBack: pSpeed = max(pSpeed - pThrust, ¬
      pTopSpeed * - 0.5)
    #brake: 
      if pSpeed > 0 then pSpeed = max(pSpeed - ¬
        pBrakePower,0)
      else if pSpeed < 0 then pSpeed = min(pSpeed ¬
        + pBrakePower, 0)
    #coast: 
      if pSpeed > 0 then pSpeed = max(0, ¬
        pSpeed - pDrag)
      else if pSpeed < 0 then pSpeed = min(0, ¬
        pSpeed + pDrag)
  end case
  
  -- apply speed to direction vector
  thisMove = thisMoveXY * pSpeed
  tempDeltaLoc = pDeltaLoc + thisMove
  newLoc = pLoc + tempDeltaLoc
  
  -- check new location & move sprite
  if inside(newLoc, pConstraintRect) then
    pDeltaLoc = tempDeltaLoc
    pSprite.loc = newLoc
    
  end if
end moveSprite

I think you'll find the motion to be more realistic, though it does not account for traction. So no matter how fast you're moving, your turns will be perfect, without the slippage that would naturally occur. That sort of calculation is much more the sort of thing that Raman Pfaff would tackle in his Physics/Lingo articles. If you're interested in that, I'd suggest you check out DOUG's Using Director archives for Raman's great articles.

Patrick McClellan is Director Online's co-founder. Pat is Vice President, Managing Director for Jack Morton Worldwide, a global experiential marketing company. He is responsible for the San Francisco office, which helps major technology clients to develop marketing communications programs to reach enterprise and consumer audiences.